BP algorithm of fully connected network 最近,由于在看论文的过程中,我发现自己对于CNN的基本结构不是很熟悉,单独抽了一段时间,强化一下自己的基础知识。我的主要参考文献是Neural Networks and Deep Learning, Michael Nielson, 原文http://neuralnetworksanddeeplearning.com/index.html
Preliminary
本篇博客内容主要是对于全连接神经网络中的BP算法进行推导,主要给出公式的推导及其值观理解
Definitions
首先,我们需要一个对于neuron的高效的标号方式,
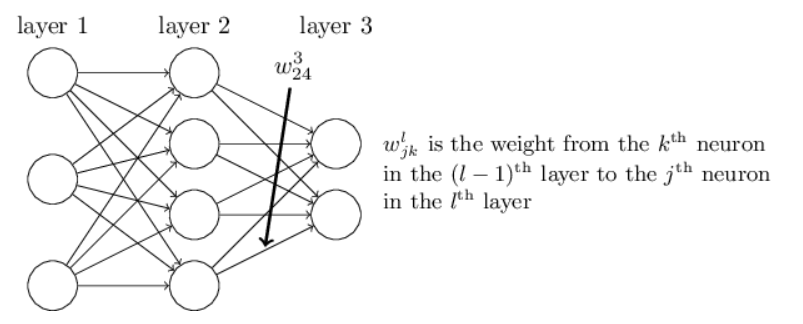
此图借鉴于Neural Networks and Deep Learning, Michael Nielson,然后,我们需要给出neuron的输入与输出间的关系, $ a^l_j=\sigma\left(\sum_kw^l_{jk}a^{l-1}_k +b^l_j\right ) $ 其中的sigma函数可以是任意激活函数,如sigmoid函数。
我们还需要给出loss函数,书中名为cost函数,此处定义为C。
BP equations
问题的核心在于求解出根据cost函数与其z之间的偏导,这是我们后续优化神经网络中各参数调整的关键,此处我们将其定义为delta。
1.引入cost函数对于$ z^l $, 即 $ z^l=w^la^{l-1}+b^l $的偏导
$ \delta^L = \frac {\partial c}{\partial a^L}\cdot \frac {\partial a^L}{\partial z^L} = \frac {\partial c}{\partial a^L}{\sigma}’\left(z^L\right)$
2.引入反向传播BP精神,将L+1层的eroor(或者说调整方向)与L层的error关联起来
$ \delta^l_j = \frac {\partial c}{\partial z^l_j} = \sum _k \frac {\partial c}{\partial z^{l+1}_k}\frac {\partial z^{l+1}_k}{\partial z^l_j} = \sum _k \delta^{l+1}_k w^{l+1}_k {\sigma}’\left(z^l\right)=\left ( w^{l+1} \right )^T\delta^{l+1}\cdot {\sigma}’\left(z^l\right) $
3.求解b的调整方式,寻找与$ \delta $之间的联系
$ \frac{\partial c}{\partial b^l_j} = \delta_j^l $
4.求解w的调整方式
$ \frac{\partial c}{\partial w^l_{jk}} = a^{l-1}_k\delta_j^l $