L1正则化与L2正则化均是我们用来防止过拟合的工具,并且,我们通常情况下会认为,L1正则化具有特征选择的作用,也即是L1正则化更倾向于将一些无关特征权重罚为0。
我们在很多书上经常会看到下面这张图(图片引用自周志华老师机器学习),用来对比L1范数与L2范数在正则化过程中的区别,L1范数更倾向于与loss函数相交于菱形可行区域的定点,即是某些特征对应权重为0处,而对于L2范数则不具备这种性质。但是,为什么L1范数具备这么好的性质那,为什么偏偏loss等值线要与菱形相交于顶点。
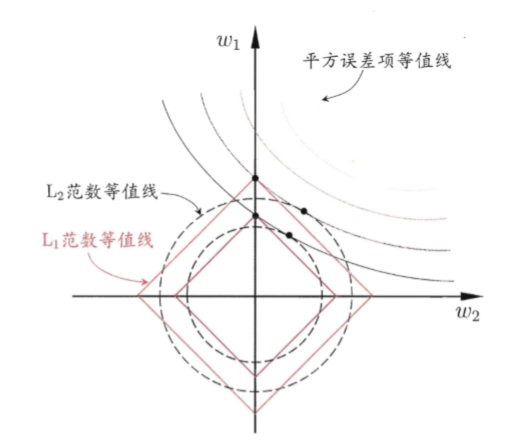
让我们拿二维情况来分析一下,首先loss的等值面都是椭圆形的,我们可以将loss函数展开看一下,y为定值时,为椭圆方程。 其次,当我们连接椭圆中心与菱形中心(坐标原点)为线段AB时,我们发现,只有当AB与菱形边界正交时,最优解存在于非顶点处;而当大多数情况下,二者无法满足正交,因此,最优解一定会坐在边界的顶点上。
但是,为什么L2正则化不存在这种性质?我们可以知道L2正则化的边界为圆形,这意味着什么那?首先,可行域边界无顶点;其次椭圆中心与圆形中心的连线始终与圆形边界正交。那么,这就使得最优解可以取在圆边界上的任意位置。