NMF Non-negative Matrix Factorization
乍一听这个名字，我一度以为这是一些纯粹的线性代数知识，然而其实是一种机器学习的理论，类似于PCA。
NMF的用途
像PCA一样，NMF主要用来作数据降维。初始数据集为一$X \in R^{n\times p}$矩阵，我们需要找到一种非负映射关系$W \in R^{p\times d}$,（注意这里的 $W$ 矩阵中所有元素非负），将原始数据 $X$ 映射至 $ R^{n\times d}$ 空间，从而将数据从 $ p $ 维降至 $d$ 维。
NMF与PCA的区别
从NMF的原理，我们可以看到其与PCA有很高的相似度。 PCA要求映射关系维所有列向量正交，这就引出了PCA的解，即利用最大特征值对应的特征向量构造 $W$ 矩阵。而这里的NMF要求 $W$ 非负，这是有物理意义的，由于计算机处理的很多信息均为非负的，例如图像，语音，我们在降维的过程中应将其映射为整数。因此，NMF对于映射矩阵 $ W $ 的要求则在于此，即所有 $W,H$ 矩阵中的元素非负， 其中 $H$ 矩阵为数据降维后的矩阵。
NMF目标函数
$min_{W,H} \frac{1}{2}\left | X-WH \right |_F^2 $[1]
$ s.t. W\geq 0,H\geq 0$
NMF用于人脸特征抽取
2001年，Lee和Seung在nature发表了一篇题为Learning the parts of objects by non-negative matrix factorization的文章[2]，在问中作者提到通过NMF进行的降维过程类似于人脑对于人脸的识别过程。作者的主要依据则为通过NMF得到的 $W$ 矩阵中的向量（特征脸）表征了人脸的局部objects，比如眼睛，眉毛，而后，我们可以通过 $H$ 矩阵将这些局部objects重构回人脸。而VQ，PCA方法得到的特征脸则均为global特征。
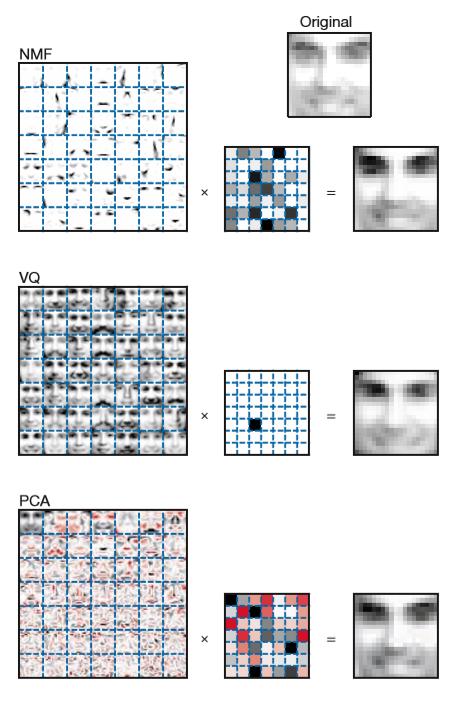处于对这一结论的好奇，我也动手去验证了，但是我得到的结果中仍然为global特征。当然，在2001年Li就提出了NMF不一定能得到局部特征[3]，并且给出了相应的理论推导。由于论文的源码和数据集均没有找到，因此验证结果仅供参考。
Referece
[1]于剑 机器学习，从公理到算法 [2]Lee, Seung, Learning the parts of objects by non-negative matrix factorization. [3]Li, Learning Spatially Localized, Parts-Based Representation.
