Preface
关于PCA,我们接触最多的是,从统计学的角度出发,去理解PCA,寻找使投影后数据间方差最大的主成分[1],经过求解可知,这些主成分就对应原始数据协方差矩阵的特征向量。而今天我要讲述的是从信息不确定度的角度出发,给出PCA的一种不同的求解方法。
基本思想
PCA在机器学习中被视为数据降维的一种实用工具,找到$d$条最能表征原始数据特征的正交向量,将原始数据集$ D\in \mathbb{R}^{m\times n}$通过投影矩阵投影至数据空间$ D\in \mathbb{R}^{m\times d}(d<n)$,使原本$n$维的数据点均用$d$维代替。
如何保证找到的$d$条正交向量能够最大程度反应原始数据信息,最经典的方法是从方差的角度去度量[1]。
而本文希望通过信息不确定度的度量方法给出正交向量的寻找方法。在信息论证,对于一个随机事件A,我们用下式来表征事件A的不确定度。
\[I(A) = -logp(A)\]在进行数据降维时,我们则希望降维后的数据不确定度最小,即低维数据点的不确定度最小,也就是说我们需要使得数据投影在我们的PCA投影向量上的概率尽可能大。
如何衡量数据$O$投影在某个方向$u$的概率?这里,我提出了以下的度量方法,
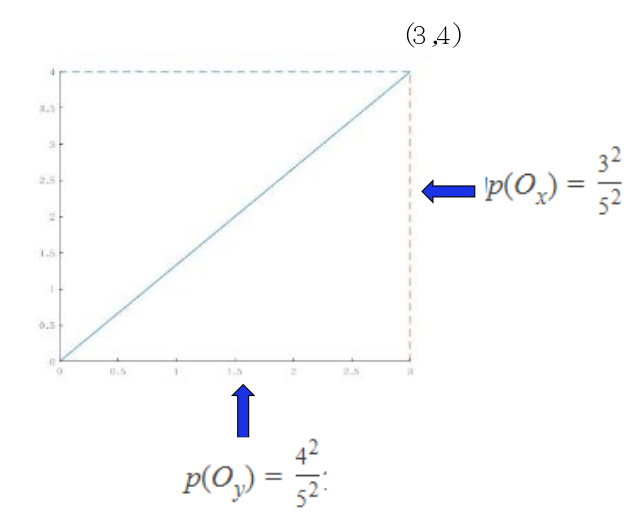
\[p(O_u) = \frac{O^T\cdot u}{\left \| O \right \|^2_2 \cdot \left \| u \right \|^2_2}\]其实这也很好理解,对于二维空间的数据点$O=(3,4) $,我们将其在$x,y$轴分别作投影,则可以得到其在两个方向的投影概率为$p(O_x) = \frac{3^2}{5^2}, p(O_y) = \frac{4^2}{5^2}$分别对应着点$O$的正弦与余弦分量。
PCA推导
-
我们这里假设先要对数据集D作归一化处理,即保证数据集的均值过坐标原点;
-
对于任意的单位方向向量$u$,有数据点$x^{(i)}$在其上的投影为${x^{(i)}}^T u$;
-
使得原始数据在方向$u$上降维后不确定度最小,即为寻找原始数据最大的投影概率所在的方向,
将上式作展开,得到
\[\begin{align*} u &= argmax_u \frac{1}{m} \sum_{i=1 } ^{m}(u^Tx^{(i)})\cdot ({x^{(i)}}^T u) \\ &= argmax _u u^T \Sigma u \end{align*}\]则此式与我们通过最大化方差相吻合,因此,投影方向应为协方差矩阵$\Sigma$特征向量所对应的方向。
Reference
[1] 高惠璇编著,应用多元统计分析,第七章 主成分分析