对图深度这个方向关注了3个月左右的时间，从零开始，一点一点的将这个方向的基础知识摸清楚。我阅读了很多文献，有Bruna的SpectralNet， Bresson的ChebNet， Kipf的GCN， Hamilton的GraphSAGE，也关注了知乎问题如何理解Graph Convolutional Network，终于能够对这一领域有一个基础的入门。回过头再来看最开始关注的这篇文章，The Emerging Field of Signal Processings on Graphs，对于Graph上的信号处理的操作又有了更好的理解。

A Brief Intro About Graphs

首先简单介绍一下Graph，Graph由顶点集合$V$与链接顶点之间的边集合$E$以及权重集合$W$构成，而这些只是Graph的拓扑信息，或者称之为domain，而每个Graph的顶点上有不同的信号或者说每个顶点上有一个函数$f(i)$。上图中展示的是无向图，即不同顶点之间的连接信息是没有方向性的，如果顶点$i$可以到达顶点$j$，则顶点$j$也一定可以到达顶点$ i $。这区别于有向图，不同顶点之间边的连接具有方向性，边上有箭头。同时，不同的边可以被赋予不同的权重，如$w_{ij}$，这些权重可以构成一个权重矩阵$ W $。

The Graph Spectral Domains

A. weighted matrix and graph signals

主要是针对一些本身不是Graph结构的数据，例如3D点云数据，图像像素的SIFT特征，如何通过构造Graph将原始数据的空间结构表现出来？进而在后续的数据处理过程中，通过考虑空间结构在内的信号处理方式，更好的对原始数据表示。这个建模问题，最关键的就是如何确定Graph上的边信息，顶点通常很好确定，如3D点云数据，每一个点可以直接作为Graph中的顶点，然而如何确定顶点与顶点之间边的信息，选择就比较多了。常见的有两种方法[1]，

计算每个顶点与其余所有顶点之间的距离度量，然后在小于某个阈值的两点之间建立边关系，如下式
建立k-NN graph，区别于聚类中的k-NN，这里指确定与某中心顶点距离度量最相近的k个其余顶点，进而确定一个k-NN Graph。这类方法在3D点云数据的处理中最常被用到，诸如DGCNN。

值得注意的是，以上提及的顶点之间的距离度量方式，可以有不同的方法，

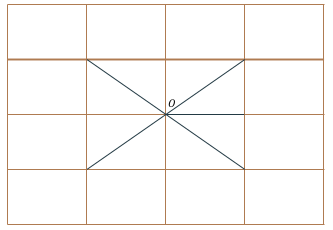
针对两顶点之间的物理距离度量，如ChebNet[3]在利用MNIST数据进行实验时，选择了8-NN的生成图的方式，而对距离的度量，则是通过不同像素点之间的物理距离实现的，对于顶点$O$，利用8-NN为其构造的相邻顶点即是图中与其连接的8个顶点，这与CNN中的3X3卷积核非常类似。
当然，采取不同顶点之间的特征空间度量距离，也是可以的。

其次，什么是graph上的信号，如同图像中每个像素点都有对应的灰度值，在图结构中，所有顶点上的信号构成了整张graph的信号。

B. Non-normalized Graph Laplacian

Laplacian算子是一个二阶差分算子，所以从它的名字，就能知道它是来干差分这个活，第一种定义是L=D-W，知乎作者Johnny Richards从热力学角度出发给出了一个很好的解释。

C. A Graph Fourier Transform and Notion of Frequency

首先来讲，为什么要对Graph上的信号进行傅氏变换，这可能跟信号处理学科的发展有关，人们在对信号进行处理时，总是会想到能否利用傅氏变换之后的频域方法实现。

类比于经典欧氏空间的傅氏变换，我们可以将信号在频域的表示，理解为原始信号在频域基底上的线性展开，而原始信号在每个基底上的成分则通过二者的内积可以求得。如(2) $\hat f(\omega)) = <f, e^{2\pi iwt}> = \int _\mathbb{R} f(t) e^{-2\pi iwt} dt \tag{2}$ 我们注意到(2)中的基底$ e^{-2\pi iwt} $ 是Laplace算子$\frac{d}{dt^2}$的特征函数(类似于特征向量，可以参考[8]中解释)。而在Graph上的Laplacian算子作为二阶差分算子，其特征向量$u_l$势必可以作为傅氏变换的一组基底，因此，有Graph上的傅氏变换如式（3）。 $f(\lambda_l)=<f, u_l> = \sum_{l=0}^{N-1} f(i)u_l^*(i) \tag{3}$ 而Laplacian矩阵的特征值$\lambda_l$则携带了与频率$\omega$类似的一些性质，下图为一传感器网络,将不同特征值对应的特征向量在原domain中展现出来,能够看到不同基底(即特征向量)代表的频率信息,这也印证了以其作为基底的合理性.注意特征值按照其大小进行标号(即$ 0=\lambda_0<\lambda_1<…<\lambda_N $),而特征向量标号与其对应.

至此,Graph上的信号有两种不同的表示形式,在原vertex domain,以及在傅氏变换后的spectral domain,这也对应于Graph Convolutional Network的两种卷积方式. 下图domain为Minnesota road graph,通过在spectral domain上定义信号傅氏变换后的形式$\hat g(\lambda_l) = e^{-5\lambda_l}$ , 将其进行逆傅氏变换则得到在vertex domain的信号表示.

D. Graph Convolution

如上文中提及,Graph上的信号在vertex domain和 spectral domain有两种表示形式,那么Graph上的卷积势必也在两个domain里有两种定义的方式.

Vertex Domain Conv

以GraphSAGE[5]为例, vertex domain的卷积是将每个顶点的邻顶点的信息aggregate到中心顶点,PATCHY-SAN中提及了CNN中Receptive Field的概念,即卷积核对应的3X3区域,而在Graph上, 通过对每个顶点建立一个Receptive Field, 然后进行aggregate.

不同于CNN,由于Graph中每个顶点邻顶点的数量通常不定,我们无法给定一个确定大小的卷积核,GraphSAGE中采取了对邻顶点进行采样的做法,将邻顶点的数量采为一个定值, 那么便可以得到一个类似于CNN的Receptive field.

通过对每个顶点建立一个恒定大小的邻域关系,可以将邻顶点的信息aggregate到中心顶点,然后与中心顶点的信息concatenate到一起,便可以实现一次卷积的操作.值得关注的是,每一次aggregate,中心顶点收集到的信息是指数倍的增长的.

Spctral Domain Conv

上文介绍了如何将信号作傅氏变换,将其变换至spectral domain,那如何在spectral domain上进行卷积操作那? 这里仍然是类比于经典欧氏空间,信号在空域的卷积与信号在频域的乘积等价,那么我们便可以利用信号在spectral domain的乘积对原信号进行卷积操作.则有如下关系式

\[\begin{align*} g &= \sum_{l=0}^{N-1} \hat f(\lambda_l) h(\lambda_l) u_l\\ &= U\begin{bmatrix} h(\lambda_0) & 0\\ ... & ...\\ 0 & h(\lambda_{N-1}) \end{bmatrix}U^T f \end{align*}\]

而后面的spectralNet, ChebeNet这些都是通过优化卷积核$H$的设计来优化网络.

References

[1] David I Shuman, Sunil K. Narang, Pascal Frossard, Antonio Ortega, Pierre Vandergheynst. The Emerging Field of Signal Processing on Graphs: Extending High-Dimensional Data Analysis to Networks and Other Irregular Domains

[2] Bruna, Zaremba, Szlam, LeCun, Spectra Networks and Deep Locally Connected Networks on Graphs

[3] Defferrard, Bresson, Vandergheynst 2016

[4] Kipf, Welling 2016

[5] William L. Hamilton. Inductive Representation Learning on Large Graphs

[6] Michael Bronstein, Joan Bruna, arthur szlam, Xavier Bresson, Yann LeCun. Geometric Deep Learning on Graphs and Manifolds

[7] DGCNN

[8] https://en.wikipedia.org/wiki/Eigenfunction

[9] PATCHY-SAN

[10] GraphhSAGE slides

Basic Elements of Graph Signal Processing